OPERASI BILANGAN BULAT POSITIF
A. PENJUMLAHAN
Penjumlahan adalah operasi untuk menambahkan dua bilangan atau lebih. Contohnya, 5 + 3 = 8. Pada penjumlahan, ada konsep barisan bilangan, penjumlahan dengan regrouping (pengelompokan), dan penggunaan algoritma penjumlahan.
1. Konsep Barisan Bilangan
Konsep penjumlahan dengan menggunakan barisan bilangan biasanya lebih sederhana dan terbatas pada barisan bilangan aritmetika dengan selisih yang tetap.
Berikut adalah konsep penjumlahan dengan menggunakan barisan bilangan:
a. Penjumlahan Barisan Aritmetika Sederhana:
Penjumlahan barisan bilangan aritmetika sederhana dilakukan dengan menggunakan bilangan bulat positif sebagai suku-suku dalam barisan.
Misalnya, penjumlahan 5 + 8 + 11 + 14 + ... dapat dihitung dengan mengenal pola bahwa setiap suku bertambah 3 dari suku sebelumnya.
Kita dapat menggunakan strategi seperti mengelompokkan suku-suku dengan selisih yang sama dan menghitung jumlahnya.
Baca Juga : Bagaimana Cara Mengerjakan Pengurangan Pecahan Biasa?
b. Menggunakan Model atau Manipulatif
Untuk membantu pemahaman konsep penjumlahan dengan menggunakan barisan bilangan, kita dapat menggunakan model atau manipulatif seperti kartu bilangan atau batang bilangan.
Kita dapat mengatur kartu bilangan atau batang bilangan secara berurutan dan menambahkan jumlahnya untuk mencari hasil penjumlahan.
c. Pola Bilangan
Konsep pola bilangan juga dapat diperkenalkan di Sekolah Dasar, di mana siswa belajar mengenali pola dalam deret bilangan.
Misalnya, siswa dapat diberikan beberapa suku dalam barisan dan diminta untuk menentukan suku berikutnya atau menemukan pola penjumlahan suku-suku tersebut.
Di Sekolah Dasar, penekanan utama adalah membangun pemahaman dasar tentang penjumlahan dalam konteks barisan bilangan aritmetika sederhana. Siswa akan dilatih untuk mengenal pola, menghitung penjumlahan dengan menggunakan rumus yang sederhana, dan menggunakan strategi yang tepat untuk menyelesaikan masalah penjumlahan barisan bilangan.
2. Penjumlahan dengan Regrouping (Pengelompokkan)
Penjumlahan dengan pengelompokkan atau regrouping di Sekolah Dasar berkaitan dengan penjumlahan bilangan bulat yang melibatkan penjumlahan di antara puluhan, ratusan, atau ribuan. Konsep ini juga dikenal sebagai penjumlahan dengan penggantian atau penyesuaian. Berikut adalah penjelasan tentang penjumlahan dengan pengelompokkan dalam konteks kelas 4 SD:
a. Penjumlahan Dalam Satu Kelompok Angka
Penjumlahan dalam satu kelompok angka terjadi saat kita menjumlahkan bilangan yang memiliki digit yang sama di posisi yang sama.
Misalnya, 34 + 27 = 61. Dalam kasus ini, kita menjumlahkan digit puluhan dan digit satuan secara terpisah.
b. Penjumlahan Dengan Pengelompokkan di Antara Digit
Penjumlahan dengan pengelompokkan di antara digit terjadi saat kita menjumlahkan bilangan yang memiliki digit berbeda di posisi yang berbeda.
Misalnya, 48 + 58 = 106. Dalam kasus ini, saat menjumlahkan digit satuan, kita perlu mengelompokkan digit puluhan jika hasil penjumlahan digit satuan melebihi 10.
Contoh Penjumlahan dengan Pengelompokkan (Regrouping):
Misalnya, kita akan menjumlahkan 46 + 58. Pada tahap penjumlahan digit satuan, hasilnya adalah 14. Namun, karena 14 melebihi 10, kita perlu melakukan pengelompokkan.
Dalam hal ini, kita memindahkan satu puluh dari digit satuan ke digit puluhan dan meninggalkan 4 di digit satuan. Akibatnya, kita mendapatkan hasil penjumlahan 1 di digit puluhan dan 4 di digit satuan, sehingga jawabannya adalah 104.
Penjumlahan dengan pengelompokkan (regrouping) penting dalam memahami konsep matematika yang lebih kompleks dan mempersiapkan siswa untuk operasi penjumlahan yang lebih lanjut. Melalui latihan dan pemahaman yang tepat, siswa dapat memperoleh keterampilan untuk menjumlahkan bilangan dengan pengelompokkan secara akurat dan efisien.
3. Penggunaan Algoritma Penjumlahan
Pada kelas Sekolah Dasar, siswa diperkenalkan dengan algoritma penjumlahan yang lebih terstruktur dan sistematis. Algoritma penjumlahan ini membantu siswa dalam menghitung penjumlahan bilangan dengan benar dan efisien. Berikut ini adalah contoh algoritma penjumlahan yang umum digunakan dalam kelas 4 SD:
a. Algoritma Penjumlahan Bertingkat
Algoritma penjumlahan bertingkat digunakan ketika dua bilangan yang akan dijumlahkan memiliki digit yang berbeda di setiap posisi.
Misalnya, saat menjumlahkan 58 + 27, algoritma bertingkat dapat digunakan sebagai berikut:
58
27
------ +
85
Algoritma ini bekerja dengan menjumlahkan digit satuan terlebih dahulu, kemudian melanjutkan ke digit puluhan jika ada. Siswa diminta untuk melakukan penjumlahan secara berurutan dari digit satuan hingga digit puluhan.
b. Algoritma Penjumlahan Tanpa Bertingkat
Algoritma penjumlahan tanpa bertingkat digunakan ketika dua bilangan yang akan dijumlahkan memiliki digit yang sama di setiap posisi.
Misalnya, saat menjumlahkan 36 + 24, algoritma tanpa bertingkat dapat digunakan sebagai berikut:
36
24
------ +
60
Algoritma ini bekerja dengan menjumlahkan digit di setiap posisi secara langsung, mulai dari digit satuan hingga digit puluhan jika ada. Tidak ada pengelompokkan atau perpindahan digit antar posisi yang terjadi.
Selama pembelajaran algoritma penjumlahan di Sekolah Dasar, siswa akan dilatih menggunakan contoh-contoh penjumlahan dalam berbagai situasi dan diberikan latihan untuk meningkatkan pemahaman dan kecakapan dalam menggunakan algoritma tersebut. Hal ini membantu siswa mengembangkan keterampilan komputasi matematika yang penting dalam kehidupan sehari-hari.
B. PENGURANGAN
Pengurangan adalah operasi untuk mengurangi satu bilangan dari bilangan lainnya. Contohnya, 8 - 3 = 5. Pada pengurangan, siswa akan belajar mengurangi bilangan dengan menggunakan pengurangan secara langsung atau dengan algoritma pengurangan.
1. Pengurangan Secara Langsung
Pada kelas 4 SD, siswa diajarkan algoritma pengurangan secara langsung untuk menghitung pengurangan bilangan dengan benar dan efisien. Algoritma ini memungkinkan siswa untuk mengurangi bilangan dengan mempertimbangkan digit di setiap posisi. Berikut adalah contoh algoritma pengurangan secara langsung yang umum digunakan di Sekolah Dasar:
a. Algoritma Pengurangan Tanpa Peminjaman (No Borrowing)
Algoritma ini digunakan ketika digit pada digit pengurangan tidak saling mempengaruhi dan pengurangan dapat dilakukan pada setiap posisi.
Misalnya, saat mengurangkan 58 - 27, algoritma tanpa peminjaman dapat digunakan sebagai berikut:
58
27
------ -
31
Algoritma ini bekerja dengan mengurangkan digit pada setiap posisi secara langsung, mulai dari digit satuan hingga digit puluhan jika ada. Tidak ada peminjaman digit yang terjadi antar posisi.
b. Algoritma Pengurangan Dengan Peminjaman (Borrowing)
Algoritma ini digunakan ketika digit pengurangan pada posisi tertentu mempengaruhi digit pada posisi sebelumnya dan membutuhkan peminjaman.
Misalnya, saat mengurangkan 36 - 24, algoritma dengan peminjaman dapat digunakan sebagai berikut:
36
24
------ -
12
Algoritma ini bekerja dengan melakukan pengurangan pada digit satuan terlebih dahulu. Jika digit pengurangan pada posisi satuan lebih kecil dari digit pengurangan pada posisi puluhan, maka siswa perlu melakukan peminjaman (atau pinjam) dari digit puluhan. Dalam contoh di atas, digit 6 pada posisi puluhan "meminjam" 1 dari digit puluhan dan dikurangi dengan 4, sehingga menghasilkan 2.
Selama pembelajaran algoritma pengurangan secara langsung di Sekolah Dasar, siswa akan diberikan contoh-contoh pengurangan dalam berbagai situasi dan dilatih untuk menggunakan algoritma tersebut. Hal ini membantu siswa mengembangkan pemahaman dan keterampilan dalam mengurangi bilangan dengan tepat dan efisien.
2. Algoritma Pengurangan
Berikut adalah algoritma pengurangan yang umum digunakan di Sekolah Dasar:
a. Algoritma Pengurangan Tanpa Peminjaman (No Borrowing)
- Tuliskan bilangan yang akan dikurangkan (pengurang) di bagian atas.
- Tuliskan bilangan yang dikurangkan (pengurangan) di bagian bawah.
- Mulai dari digit satuan (digit paling kanan), kurangkan digit pada posisi yang sama secara langsung.
- Jika hasil pengurangan pada posisi tersebut tidak melebihi 9, tulis hasil pengurangan tersebut.
- Jika hasil pengurangan pada posisi tersebut melebihi 9, tulis satu digit hasil pengurangan dan "bungkus" (carry over) ke digit sebelumnya.
- Ulangi langkah 3 hingga 5 untuk digit pada posisi puluhan, ratusan, dan seterusnya jika ada.
- Jika semua digit telah dikurangkan, tulis hasil pengurangan di bawah garis.
Contoh:
82
17
------ -
65
Baca Juga : Bagaimana Cara Penjumlahan Pecahan Desimal?
b. Algoritma Pengurangan Dengan Peminjaman (Borrowing)
- Tuliskan bilangan yang akan dikurangkan (pengurang) di bagian atas.
- Tuliskan bilangan yang dikurangkan (pengurangan) di bagian bawah.
- Mulai dari digit satuan (digit paling kanan), kurangkan digit pada posisi yang sama secara langsung.
- Jika hasil pengurangan pada posisi tersebut tidak negatif, tulis hasil pengurangan tersebut.
- Jika hasil pengurangan pada posisi tersebut negatif, cari digit sebelumnya yang dapat "dipinjam".
- Kurangkan digit pinjaman dengan 1 dan tambahkan 10 ke hasil pengurangan pada posisi sekarang.
- Tulis hasil pengurangan yang telah dikoreksi pada posisi sekarang.
- Ulangi langkah 3 hingga 7 untuk digit pada posisi puluhan, ratusan, dan seterusnya jika ada.
- Jika semua digit telah dikurangkan, tulis hasil pengurangan di bawah garis.
Contoh:
54
27
------ -
27
Selama pembelajaran algoritma pengurangan di Sekolah Dasar, siswa akan diberikan contoh-contoh pengurangan dalam berbagai situasi dan dilatih untuk menggunakan algoritma tersebut. Hal ini membantu siswa mengembangkan pemahaman dan keterampilan dalam mengurangi bilangan dengan tepat dan efisien.
C. PERKALIAN
Perkalian adalah operasi untuk menggandakan atau mengulang suatu bilangan dengan bilangan lain. Contohnya, 4 x 2 = 8. Dalam perkalian, siswa akan mempelajari konsep dasar perkalian, tabel perkalian, perkalian dengan nol, dan penggunaan algoritma perkalian.
1. Konsep Dasar Perkalian
Konsep dasar perkalian yang diajarkan di Sekolah Dasar berfokus pada pemahaman perkalian sebagai pengulangan penjumlahan bilangan yang sama. Berikut adalah beberapa konsep dasar perkalian yang diajarkan pada tingkat ini:
a. Pengertian Perkalian:
Perkalian adalah operasi matematika untuk menggandakan atau mengulang bilangan sebanyak faktor yang ditentukan.
Misalnya, perkalian 3 × 4 berarti menggandakan bilangan 3 sebanyak 4 kali atau mengulangi penjumlahan 3 + 3 + 3 + 3.
b. Menggunakan Tabel Perkalian (Perkalian Dasar)
Siswa diperkenalkan dengan tabel perkalian dasar (sering disebut juga sebagai tabel perkalian atau tabel kali).
Tabel ini berisi hasil perkalian dari angka 1 hingga 10, seperti 1 × 1 = 1, 1 × 2 = 2, 1 × 3 = 3, dan seterusnya.
Siswa diajarkan untuk menggunakan tabel ini sebagai referensi dalam mencari hasil perkalian yang diperlukan.
c, Sifat Komutatif Perkalian
Siswa mempelajari sifat komutatif dalam perkalian, yang berarti urutan faktor tidak mempengaruhi hasil perkalian.
Misalnya, 3 × 4 dan 4 × 3 akan menghasilkan hasil perkalian yang sama, yaitu 12.
d. Menggunakan Model Visual
Siswa juga dapat menggunakan model visual seperti array persegi atau garis-garis untuk mengilustrasikan konsep perkalian.
Misalnya, dengan menggunakan array persegi, siswa dapat memahami konsep perkalian sebagai pengulangan baris dan kolom yang sama untuk menentukan jumlah keseluruhan.
Menerapkan Perkalian dalam Konteks Masalah:
Siswa diajarkan untuk menerapkan konsep perkalian dalam konteks masalah sehari-hari, seperti menghitung jumlah barang yang sama, menghitung keliling atau luas persegi panjang, dan sebagainya.
Melalui pembelajaran konsep dasar perkalian ini, siswa Sekolah Dasar memperoleh pemahaman tentang arti perkalian, menguasai tabel perkalian dasar, dan mampu menerapkan perkalian dalam situasi praktis. Hal ini membantu mereka membangun landasan yang kuat untuk perkalian yang lebih kompleks di tingkat berikutnya.
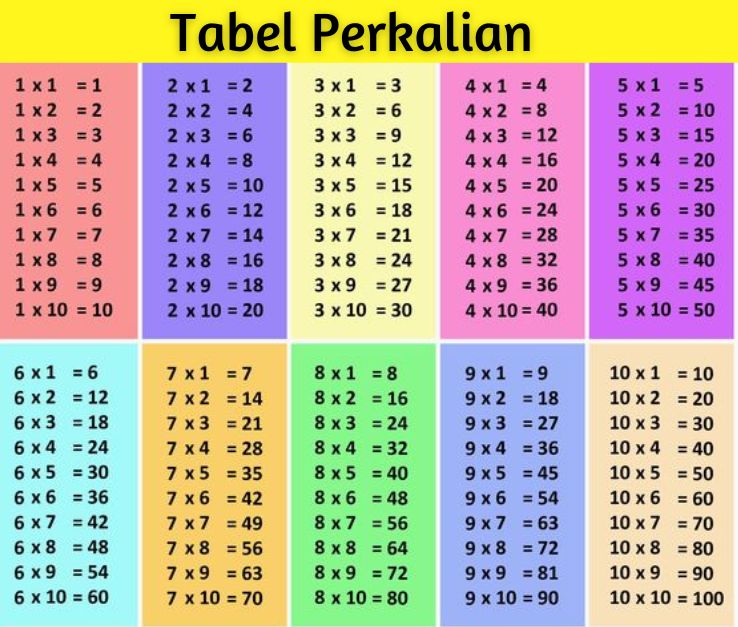
2. Tabel Perkalian
Berikut adalah contoh tabel perkalian dasar yang sering diajarkan di Sekolah Dasar:
Tabel perkalian ini membantu siswa Sekolah Dasar dalam menghafal dan menguasai hasil perkalian dasar dengan lebih mudah. Melalui latihan dan penggunaan tabel ini, siswa dapat memperkuat pemahaman mereka tentang perkalian dan memperoleh kecakapan dalam mengaplikasikan perkalian dalam pemecahan masalah matematika.
3. Perkalian dengan Nol
Di Sekolah Dasar, siswa diajarkan tentang konsep perkalian dengan nol. Berikut adalah beberapa konsep dasar yang terkait dengan perkalian dengan nol:
a. Sifat Perkalian dengan Nol
Perkalian dengan nol memiliki sifat khusus, yaitu hasil perkalian apapun dengan nol akan selalu menghasilkan nol.
Misalnya, 5 × 0 = 0, 10 × 0 = 0, 100 × 0 = 0, dan seterusnya.
b. Arti Perkalian dengan Nol
Perkalian dengan nol dapat diartikan sebagai pengelompokan atau penjumlahan bilangan nol sebanyak faktor yang ditentukan.
Misalnya, 3 × 0 dapat diartikan sebagai mengelompokkan atau menjumlahkan bilangan 0 sebanyak 3 kali, yang hasilnya tetap 0.
Contoh Penggunaan Perkalian dengan Nol:
Dalam konteks masalah, perkalian dengan nol dapat digunakan untuk menghitung hasil perkalian ketika salah satu faktornya adalah nol.
Misalnya, dalam sebuah kelompok terdapat 0 kelereng, jika setiap kelompok terdiri dari 5 anak, maka jumlah kelereng keseluruhan dalam kelompok tersebut adalah 0 × 5 = 0.
Pemahaman tentang perkalian dengan nol penting karena nol adalah bilangan yang muncul secara luas dalam konteks matematika dan dunia nyata. Dengan memahami konsep ini, siswa Sekolah Dasar dapat mengaplikasikan perkalian dengan nol secara tepat dalam pemecahan masalah dan membangun pemahaman yang lebih kokoh tentang operasi perkalian secara umum.
4. Penggunaan Algoritma Perkalian
Algoritma perkalian yang umum diajarkan di Sekolah Dasar adalah algoritma perkalian secara berurutan. Berikut adalah algoritma tersebut:
a. Algoritma Perkalian Secara Berurutan
- Tuliskan bilangan pertama (faktor pertama) di bagian atas.
- Tuliskan bilangan kedua (faktor kedua) di bagian bawah.
- Mulai dari digit satuan (digit paling kanan) pada bilangan kedua, kalikan digit tersebut dengan semua digit pada bilangan pertama.
- Tulis hasil perkalian di bawah garis.
- Geser satu digit ke kiri pada bilangan kedua dan ulangi langkah 3 hingga 4 untuk digit selanjutnya.
Jika semua digit pada bilangan kedua telah dikalikan, tambahkan semua hasil perkalian yang ditulis di bawah garis untuk mendapatkan hasil perkalian akhir.
Contoh:
24
3
------ ×
72
Pada algoritma ini, siswa diminta untuk melakukan perkalian berurutan dari digit-digit pada faktor kedua dengan semua digit pada faktor pertama. Hasil perkalian pada setiap posisi digit ditulis di bawah garis dan diakumulasikan untuk mendapatkan hasil akhir.
Melalui latihan menggunakan algoritma ini, siswa Sekolah Dasar dapat memperoleh kecakapan dalam melakukan perkalian dengan angka dua digit secara berurutan dan memahami proses perkalian secara keseluruhan.
D. PEMBAGIAN
Pembagian adalah operasi untuk membagi suatu bilangan menjadi bagian-bagian yang sama besar. Contohnya, 12 ÷ 3 = 4. Pada pembagian, siswa akan belajar tentang konsep dasar pembagian, pembagian dengan hasil sisa (sisa pembagian), dan penggunaan algoritma pembagian.
1. Konsep Dasar Pembagian
Konsep dasar pembagian yang diajarkan di Sekolah Dasar meliputi pemahaman tentang pembagian sebagai pembagian objek dalam kelompok yang sama. Berikut adalah beberapa konsep dasar pembagian yang diajarkan pada tingkat ini:
a. Pembagian sebagai Pembagian Objek
Pembagian adalah operasi matematika untuk membagi objek atau jumlah tertentu menjadi kelompok yang sama besar.
Misalnya, jika ada 12 kelereng yang akan dibagi menjadi 4 kelompok, setiap kelompok akan mendapatkanc 3 kelereng.
b. Notasi Pembagian
Dalam notasi pembagian, tanda pembagian yang digunakan adalah tanda ":" atau garis miring ("/").
Misalnya, 12 : 4 atau 12 / 4 adalah notasi untuk membagi 12 menjadi 4 kelompok.
c. Menggunakan Model Visual
Siswa dapat menggunakan model visual, seperti gambar atau manipulatif matematika, untuk membantu memahami konsep pembagian.
Misalnya, siswa dapat menggunakan benda fisik, seperti blok matematika, untuk menggambarkan pembagian dengan membagi objek secara fisik menjadi kelompok yang sama.
d. Memahami Istilah dalam Pembagian
Dalam pembagian, istilah-istilah yang umum digunakan adalah: pembagi (divisor), pembagian (division), pembagian yang tidak sama (unequal division), dan sisa (remainder).
Misalnya, dalam pembagian 12 : 4, 12 adalah dividennya, 4 adalah divisor (pembagi), hasil pembagian adalah quotient (pembagian), dan jika tidak ada sisa, pembagian dikatakan "pembagian yang sama" (equal division).
e. Penerapan Pembagian dalam Konteks Masalah
Siswa diajarkan untuk menerapkan konsep pembagian dalam konteks masalah sehari-hari, seperti membagi barang, membagi makanan, membagi waktu, dan sebagainya.
Melalui pembelajaran konsep dasar pembagian ini, siswa Sekolah Dasar memperoleh pemahaman tentang arti pembagian, mengembangkan kemampuan membagi objek menjadi kelompok yang sama, dan mampu menerapkan pembagian dalam situasi praktis. Hal ini membantu mereka membangun landasan yang kuat untuk pembagian yang lebih kompleks di tingkat berikutnya.
2. Pembagian dengan Hasil Sisa (Sisa Pembagian)
Pembagian dengan hasil sisa, yang juga dikenal sebagai pembagian dengan sisa pembagian, adalah pembagian di mana setelah pembagian selesai, masih ada sisa yang tidak dapat dibagi habis. Konsep ini sering diajarkan di Sekolah Dasar ketika siswa sudah memahami pembagian dasar dan sifat pembagian.
Contoh: Misalkan kita memiliki 13 kelereng yang akan dibagi menjadi 4 kelompok yang sama besar. Bagaimana cara membagi 13 kelereng tersebut?
Langkah-langkah pembagian dengan hasil sisa:
- Bagi kelereng satu per satu secara merata ke dalam 4 kelompok sampai tidak ada kelereng lagi.
- Setelah membagi 3 kelereng, 1 kelereng tersisa, dan tidak dapat dibagi lagi secara merata.
- Hasil pembagian dengan hasil sisa adalah 3 kelereng untuk setiap kelompok dan sisa 1 kelereng.
Notasi matematika untuk pembagian dengan hasil sisa adalah sebagai berikut: 13 : 4 = 3 dengan sisa 1
Artinya, ketika 13 kelereng dibagi dengan 4 kelompok, setiap kelompok akan mendapatkan 3 kelereng, dan ada 1 kelereng yang tersisa.
Dalam matematika, sisa pembagian ini sering dinyatakan sebagai "sisa" atau "modulus" (dalam simbol matematika disebut dengan tanda persen "%"). Sisa pembagian dapat digunakan dalam berbagai konteks, seperti dalam pemecahan masalah matematika, ilmu komputer, dan berbagai bidang lainnya.
3. Penggunaan Algoritma Pembagian
Di Sekolah Dasar, siswa diajarkan untuk menggunakan algoritma pembagian untuk membagi bilangan dengan pembagian yang sama atau dengan hasil sisa. Algoritma pembagian adalah cara langkah-demi-langkah untuk melakukan pembagian dengan sistematis. Berikut adalah algoritma pembagian yang umum digunakan:
a.Algoritma Pembagian
- Tuliskan bilangan yang akan dibagi (dividen) di atas garis pembagian.
- Tuliskan bilangan pembagi (divisor) di bawah garis pembagian.
- Mulai dari digit paling kiri pada bilangan dividen, tentukan berapa kali bilangan pembagi dapat masuk ke dalam dividen secara utuh (tanpa sisa).
- Tulis angka hasil pembagian di atas garis, tepat di atas digit yang sedang dihitung.
- Kalikan angka pembagi dengan angka hasil pembagian, dan tulis hasil perkalian di bawah digit yang dihitung sebelumnya.
- Kurangkan hasil perkalian dari digit yang sedang dihitung. Tulis hasil pengurangan di bawah angka hasil perkalian.
- Geser ke digit selanjutnya pada bilangan dividen dan ulangi langkah 3 hingga 6 hingga semua digit pada dividen telah dihitung.
- Jika ada sisa setelah melakukan semua langkah, tuliskan sisa tersebut di bawah garis sebagai hasil sisa pembagian.
Contoh: Misalkan kita akan membagi 132 dengan 4.
4 | 132 = 33
12
-------- -
012
12
-------- -
0
Hasil pembagian adalah 33 dengan hasil sisa 0. Artinya, 132 dibagi dengan 4 menghasilkan 33 tanpa sisa.
Algoritma pembagian ini membantu siswa Sekolah Dasar dalam memahami dan melaksanakan pembagian dengan sistematis. Dengan latihan yang cukup, siswa dapat memperoleh kecakapan dalam melakukan pembagian baik dengan pembagian yang sama maupun pembagian dengan hasil sisa.
Selama pembelajaran bilangan bulat, siswa akan mempelajari strategi dan teknik yang tepat untuk menyelesaikan masalah matematika yang melibatkan penjumlahan, pengurangan, perkalian, dan pembagian. Selain itu, siswa juga akan melatih keterampilan berpikir kritis, pemecahan masalah, dan pemahaman konsep matematika melalui latihan-latihan dan aktivitas yang relevan.
Baca Juga : Bagaimana Cara Pengurangan Bilangan Desimal?